(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系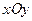 内,点
内,点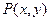 在曲线C:
在曲线C: 为参数,
为参数,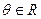 )上运动.以
)上运动.以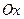 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线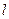 的极坐标方程为
的极坐标方程为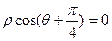 .
.
(Ⅰ) 写出曲线C的标准方程和直线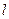 的直角坐标方程;
的直角坐标方程;
(Ⅱ) 若直线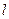 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求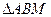 面积的
面积的
最大值.
推荐套卷
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系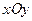 内,点
内,点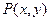 在曲线C:
在曲线C: 为参数,
为参数,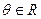 )上运动.以
)上运动.以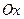 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线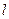 的极坐标方程为
的极坐标方程为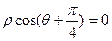 .
.
(Ⅰ) 写出曲线C的标准方程和直线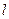 的直角坐标方程;
的直角坐标方程;
(Ⅱ) 若直线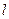 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求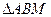 面积的
面积的
最大值.