三角形 的三个内角
的三个内角 、
、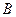 、
、 的对边的长分别为
的对边的长分别为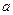 、
、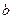 、
、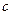 ,有下列两个条件:(Ⅰ)
,有下列两个条件:(Ⅰ)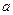 、
、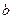 、
、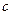 成等差数列;(Ⅱ)
成等差数列;(Ⅱ)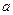 、
、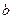 、
、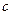 成等比数列。
成等比数列。
现给出三个结论:
① ;②
;② ;③
;③ .
.
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之
推荐套卷
三角形 的三个内角
的三个内角 、
、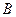 、
、 的对边的长分别为
的对边的长分别为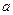 、
、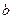 、
、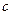 ,有下列两个条件:(Ⅰ)
,有下列两个条件:(Ⅰ)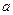 、
、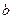 、
、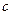 成等差数列;(Ⅱ)
成等差数列;(Ⅱ)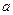 、
、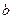 、
、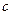 成等比数列。
成等比数列。
现给出三个结论:
① ;②
;② ;③
;③ .
.
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之