在上海世界博览会开展期间,计划选派部分高二学生参加宣传活动,报名参加的学生需进行测试,共设4道选择题,规定必须答完所有题,且答对一题得1分,答错一题扣1分,至少得2分才能入选成为宣传员;甲乙丙三名同学报名参加测试,他们答对每个题的概率都为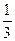 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.
(1)用随机变量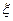 表示能够成为宣传员的人数,求
表示能够成为宣传员的人数,求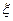 的数学期望与方差;
的数学期望与方差;
(2)若学生甲得分的数值为随机变量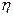 ,求所得分数
,求所得分数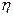 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
在上海世界博览会开展期间,计划选派部分高二学生参加宣传活动,报名参加的学生需进行测试,共设4道选择题,规定必须答完所有题,且答对一题得1分,答错一题扣1分,至少得2分才能入选成为宣传员;甲乙丙三名同学报名参加测试,他们答对每个题的概率都为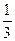 ,且每个人答题相互不受影响.
,且每个人答题相互不受影响.
(1)用随机变量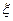 表示能够成为宣传员的人数,求
表示能够成为宣传员的人数,求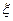 的数学期望与方差;
的数学期望与方差;
(2)若学生甲得分的数值为随机变量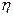 ,求所得分数
,求所得分数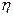 的分布列和数学期望.
的分布列和数学期望.