（本小题满分15分）
如图，已知抛物线
的准线为
，
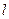为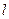上的一个动点，过点作抛物
线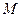
的两条切线，切点分别为
，
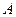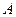，再分别过，两点作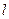的垂线，垂足分别为
，
．
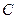（1）求证：直线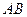
必经过
轴上的一个定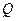点
，并写出点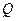的坐标；
（2）若
，
，
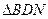的面积依次构成等差数列，求此时点的坐标．
相关试题
满足
,数列
满足
。
的前
项和；
，求数列
的前
的三内角
、
、
所对的边分别是
，
，
，且
，求
的值；
的三内角
、
、
所对的边分别是
，
，
，向量
，且
。
，求
的范围。
，
；
。
。
时，①求函数
的单调区间；②求函数
处的切线方程；
既有极大值，又有极小值，且当
时，
恒成立，求
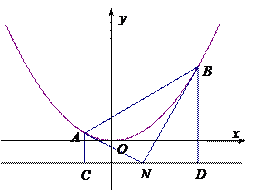
的取值范围.相关知识点
推荐套卷
（本小题满分15分）
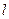如图，已知抛物线的准线为，为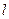上的一个动点，过点作抛物
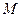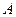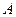线的两条切线，切点分别为，，再分别过，两点作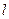的垂线，垂足分别为，．
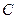（1）求证：直线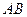必经过轴上的一个定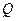点，并写出点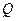的坐标；
（2）若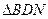，，的面积依次构成等差数列，求此时点的坐标．
粤公网安备 44130202000953号