2008年奥运会的一套吉祥物有五个,分别命名:“贝贝”、 “晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此
“晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此 前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为
前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为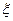 .
.
(1)求掷骰子的次数为7的概率;
(2)求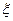 的分布列及数学期望E
的分布列及数学期望E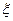 .
.
推荐套卷
2008年奥运会的一套吉祥物有五个,分别命名:“贝贝”、 “晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此
“晶晶”、“欢欢”、“迎迎”和“妮妮”,称“奥运福娃”。甲、乙两位小学生各有一套吉祥物,现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲将赢得乙一个福娃;否则乙赢得甲一个福娃。现规定掷骰子的总次数达9次时,或在此 前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为
前某学生已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的总次数为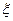 .
.
(1)求掷骰子的次数为7的概率;
(2)求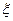 的分布列及数学期望E
的分布列及数学期望E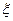 .
.