18．（本小题满分14分）
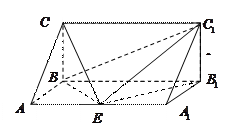
一个三棱柱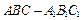
直观图和三视图如图所示（主视图、俯视图都是矩形，左视图是直角三角形），设
、
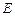分别为
和
的中点．
（Ⅰ）求几何体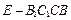
的体积；
（Ⅱ）证明：
平面
；
（Ⅲ）证明：平面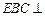
平面
.
，求x，y的值，使
，且
．
三向量两两所成的角相等，并且
，
，
，试求向量
的长度以及与已知三向量的夹角.
=（
，-1）和
=（1，
的向量的坐标.
所成的比λ.
，线段AB的中点为M，
相关知识点
推荐套卷
18．（本小题满分14分）
一个三棱柱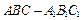直观图和三视图如图所示（主视图、俯视图都是矩形，左视图是直角三角形），设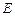、分别为和的中点．
（Ⅰ）求几何体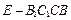的体积；
（Ⅱ）证明：平面；
（Ⅲ）证明：平面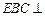平面.
粤公网安备 44130202000953号