（从22/23/24三道解答题中任选一道作答，作答时，请注明题号；若多做，则按首做题计入总分，满分10分. 请将答题的过程写在答题卷中指定的位置）（本小题满分10分）选修4—4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的
轴的正半轴重合．直线
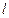的参数方程是
（
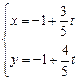为参数），曲线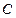
的极坐标方程为
．
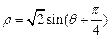（Ⅰ）求曲线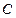的直角坐标方程；
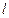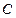（Ⅱ）设直线与曲线相交于
，
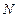两点，求M,N两点间的距离．
相关试题
当
时，求函数
的最小值；
为实数，函数
，若
，求函数
在
上的最大值和最小值。
，
，求实数
的值；
，求实数
满足
，求
;又若
，求
;
，使得
，求函数
，
，当x＞0时，
，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.推荐套卷
（从22/23/24三道解答题中任选一道作答，作答时，请注明题号；若多做，则按首做题计入总分，满分10分. 请将答题的过程写在答题卷中指定的位置）（本小题满分10分）选修4—4：坐标系与参数方程
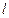已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的轴的正半轴重合．直线的参数方程是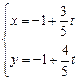（为参数），曲线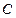的极坐标方程为．
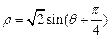（Ⅰ）求曲线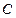的直角坐标方程；
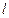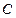（Ⅱ）设直线与曲线相交于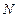，两点，求M,N两点间的距离．
粤公网安备 44130202000953号