某工厂2010年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加四月份的一个展销会：
（1）问A、B、C、D型号的产品各抽取多少件？
（2）从50件样品随机的抽取2件，求这2件产品恰好是不同型号产品的概率；
（3）从A、C型号的产品中随机的抽取3件，用
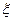表示抽取A种型号的产品件数，求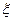的分布列和数学期望。
相关试题
；
．
；
，y），且sinα=
y（y≠0），判断角α所在的象限，并求cosα和tanα的值．推荐套卷
某工厂2010年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加四月份的一个展销会：
（1）问A、B、C、D型号的产品各抽取多少件？
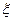（2）从50件样品随机的抽取2件，求这2件产品恰好是不同型号产品的概率； （3）从A、C型号的产品中随机的抽取3件，用表示抽取A种型号的产品件数，求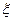的分布列和数学期望。
粤公网安备 44130202000953号