(本小题满分12分)已知抛物线 :
: (
(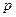 为正常数)的焦点为
为正常数)的焦点为 ,过
,过 做一直线
做一直线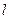 交抛物线
交抛物线 于
于
 ,
,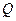 两点,点
两点,点 为坐标原点.
为坐标原点.
(1)若 的面积记为
的面积记为 ,求
,求 的值;
的值;
(2)若直线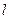 垂直于
垂直于 轴,过点P做关于直线
轴,过点P做关于直线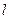 对称的两条直线
对称的两条直线 ,
, 分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
推荐套卷
(本小题满分12分)已知抛物线 :
: (
(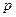 为正常数)的焦点为
为正常数)的焦点为 ,过
,过 做一直线
做一直线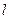 交抛物线
交抛物线 于
于
 ,
,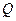 两点,点
两点,点 为坐标原点.
为坐标原点.
(1)若 的面积记为
的面积记为 ,求
,求 的值;
的值;
(2)若直线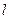 垂直于
垂直于 轴,过点P做关于直线
轴,过点P做关于直线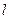 对称的两条直线
对称的两条直线 ,
, 分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.
分别交抛物线C于M,N两点,证明:直线MN斜率等于抛物线在点Q处的切线斜率.