(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为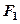 、
、 ,其中
,其中 也是抛物线
也是抛物线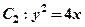 的焦点,M是
的焦点,M是 与
与 在第一象限的交点,且
在第一象限的交点,且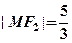 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知菱形ABCD的顶点A﹑C在椭圆 上,顶点B﹑D在直线
上,顶点B﹑D在直线 上,求直线AC的方程.
上,求直线AC的方程.
推荐套卷
(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为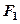 、
、 ,其中
,其中 也是抛物线
也是抛物线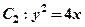 的焦点,M是
的焦点,M是 与
与 在第一象限的交点,且
在第一象限的交点,且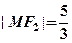 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知菱形ABCD的顶点A﹑C在椭圆 上,顶点B﹑D在直线
上,顶点B﹑D在直线 上,求直线AC的方程.
上,求直线AC的方程.