(本小题满分12分)某人上楼梯,每步上一阶的概率为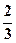 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第n阶的概率为
,设该人从台阶下的平台开始出发,到达第n阶的概率为 。
。
(Ⅰ)求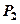 ;(Ⅱ)该人共走了5步,求
;(Ⅱ)该人共走了5步,求 该人这5步共上的阶数ξ的数学期望。
该人这5步共上的阶数ξ的数学期望。
相关知识点
推荐套卷
(本小题满分12分)某人上楼梯,每步上一阶的概率为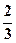 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第n阶的概率为
,设该人从台阶下的平台开始出发,到达第n阶的概率为 。
。
(Ⅰ)求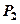 ;(Ⅱ)该人共走了5步,求
;(Ⅱ)该人共走了5步,求 该人这5步共上的阶数ξ的数学期望。
该人这5步共上的阶数ξ的数学期望。