要制作一个由同底圆锥和圆柱组成的储油罐（如图），设计要求：圆锥和圆柱的总高度和圆柱底面半径相等，都为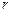
米.市场上，圆柱侧面用料单价为每平方米
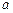元，圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
（弧度），总费用为
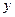（元）.
（1）写出的取值范围；（2）将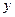表示成的函数关系式；
（3）当为何值时，总费用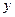最小?
相关试题
},集合B={（x,y）
,且0
}，又A
，求实数m的取值范围.
)上单调递增，并且f (x)<0对一切
成立，试判断
在(－
，且
，求证：
．
+x－6=0｝，B=｛x | mx+1=0｝，若B
A，求由实数m所构成的集合M．
满足
，
． 
，求证：数列
为等比数列；
的最小正整数
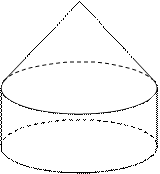
推荐套卷
要制作一个由同底圆锥和圆柱组成的储油罐（如图），设计要求：圆锥和圆柱的总高度和圆柱底面半径相等，都为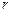米.市场上，圆柱侧面用料单价为每平方米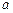元，圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为（弧度），总费用为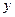（元）.
（1）写出的取值范围；（2）将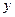表示成的函数关系式；
（3）当为何值时，总费用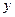最小?
粤公网安备 44130202000953号