(本小题满分12分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有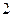 人,会跳舞的
人,会跳舞的
有 人,现从中任选
人,现从中任选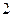 人.设
人.设 为选出的人中既会唱歌又会跳舞的人数,
为选出的人中既会唱歌又会跳舞的人数, .
.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出 的概率分布列并计算
的概率分布列并计算 .
.
推荐套卷
(本小题满分12分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有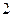 人,会跳舞的
人,会跳舞的
有 人,现从中任选
人,现从中任选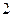 人.设
人.设 为选出的人中既会唱歌又会跳舞的人数,
为选出的人中既会唱歌又会跳舞的人数, .
.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出 的概率分布列并计算
的概率分布列并计算 .
.