(本小题满分13分)
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(Ⅰ)求4人恰好选择了同一家公园的概率;
(Ⅱ)设选择甲公园的志愿者的人数为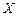 ,试求
,试求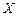 的分布列及期望.
的分布列及期望.
推荐套卷
(本小题满分13分)
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(Ⅰ)求4人恰好选择了同一家公园的概率;
(Ⅱ)设选择甲公园的志愿者的人数为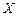 ,试求
,试求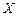 的分布列及期望.
的分布列及期望.