（本小题满分12分）
如图，A、B分别是椭圆
的公共左右顶点，P、Q分别位于椭圆和双曲线上且不同于A、B的两点，设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
（1）求证：O、P、Q三点共线；（O为坐标原点）
（2）设F1、F2分别是椭圆和双曲线的右焦点，已知PF1//QF2，求
的值。
，集合
，求
．
，
，求证：
．
随时间
变化的函数为
．
时的电流强度．
，
：
经过怎样的变换，得到该函数的图象．
且
．求
的值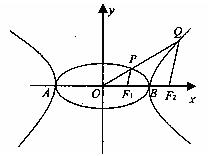．推荐套卷
（本小题满分12分）
如图，A、B分别是椭圆的公共左右顶点，P、Q分别位于椭圆和双曲线上且不同于A、B的两点，设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
（1）求证：O、P、Q三点共线；（O为坐标原点）
（2）设F1、F2分别是椭圆和双曲线的右焦点，已知PF1//QF2，求的值。
粤公网安备 44130202000953号