（本小题满分16分）已知椭圆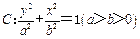
的离心率为
，过右顶点A的直线l与椭圆C相交于A、B两点，且
.
（1）求椭圆C和直线l的方程；
（2）记曲线C在直线l下方的部分与线段AB所围成的平面区域（含边界）为D．若曲线
与D有公共点，试求实数m的最小值．
.求 圆C的方程.
(常数
.
时，求曲线
在点
处的切线方程；
在区间
上零点的个数（
为自然对数的底数）.
首项
，前
项和
与
之间满足
是等差数列
，使
对于一切
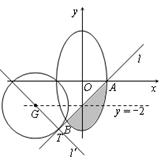
都成立，求推荐套卷
（本小题满分16分）已知椭圆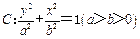的离心率为，过右顶点A的直线l与椭圆C相交于A、B两点，且.
（1）求椭圆C和直线l的方程；
（2）记曲线C在直线l下方的部分与线段AB所围成的平面区域（含边界）为D．若曲线与D有公共点，试求实数m的最小值．
粤公网安备 44130202000953号