(本小题满分14分)
在直角坐标系xOy中,已知圆心在第二象限、半径为2 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为10。
与圆C的一个交点到椭圆两焦点的距离之和为10。
(1)求圆C的方程;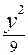
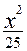 (2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
OF的长,若存在求出Q的坐标;若不存在,请说明理由。
推荐套卷
(本小题满分14分)
在直角坐标系xOy中,已知圆心在第二象限、半径为2 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为10。
与圆C的一个交点到椭圆两焦点的距离之和为10。
(1)求圆C的方程;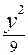
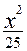 (2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
OF的长,若存在求出Q的坐标;若不存在,请说明理由。