（本小题满分12分）
如图，在棱长为1的正方体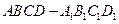
中，
是侧棱
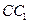上的一点，
．
（１） 试确定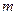
，使直线
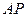与平面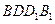
所成角的正切值为
；
（２） 在线段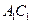
上是否存在一个定点
，
使得对任意的，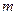
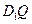在平面
上
的射影垂直于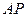，并证明你的结论．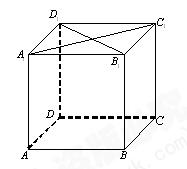
相关试题
在一个周期内，当
时，
取得最小值
；当
时，
，再将图像沿
轴向右平移
个单位，得到函数
的图像.
.
上的值域.
，面积
，求这个扇形的半径
和圆心角
的弧度数.
，
.
时，求不等式
的解集；
对
恒成立，求实数
的取值范围.推荐套卷
（本小题满分12分）
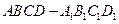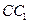如图，在棱长为1的正方体中，是侧棱上的一点，．
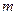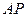（１） 试确定，使直线与平面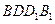
所成角的正切值为；
（２） 在线段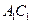上是否存在一个定点，
使得对任意的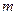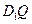，在平面上
的射影垂直于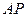，并证明你的结论．
粤公网安备 44130202000953号