a11,a12,……a18
a21,a22,……a28
…………………
a81,a82,……a88
64个正数排成8行8列, 如上所示:在符合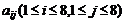 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且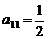 ,
,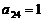 ,
, 。
。
⑴若 ,求
,求 和
和 的值。
的值。
⑵记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足 ,联
,联 (m为非零常数),
(m为非零常数), ,且
,且 ,求
,求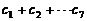 的取值范围。
的取值范围。
⑶对⑵中的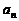 ,记
,记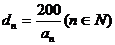 ,设
,设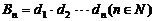 ,求数列
,求数列 中最大项的项数。
中最大项的项数。
推荐套卷
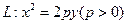 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
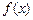 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。 (2)若矩形ABCD的一个边AB="3," 另一边BC=2
(2)若矩形ABCD的一个边AB="3," 另一边BC=2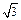 ,EF=2
,EF=2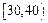

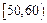
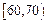

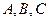 是
是 的三个内角,已知向量
的三个内角,已知向量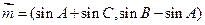 ,
,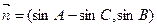 ,且
,且 .
.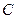 的大小; (Ⅱ)若向量
的大小; (Ⅱ)若向量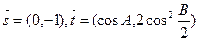 ,试求
,试求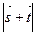 的取值范围
的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号