某单位决定投资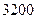
元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米造价
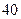元，两侧墙砌砖，每米造价
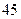元，顶部每平方米造价
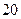元，试问：（1）仓库面积
的最大允许值是多少？（2）为使达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？
）（A＞0，ω＞0，|
）图象的一部分，试求出其解析式.
的定义域.推荐套卷
某单位决定投资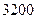元建一仓库（长方体状），高度恒定，它的后墙利用旧墙不花钱，正面用铁栅，每米造价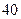元，两侧墙砌砖，每米造价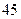元，顶部每平方米造价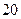元，试问：（1）仓库面积的最大允许值是多少？（2）为使达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？
粤公网安备 44130202000953号