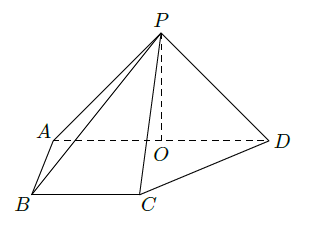
在四棱锥
中,侧面
底面
,侧棱
,底面
为直角梯形,其中
为
中点.
(Ⅰ)求证:
平面
;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点
到平面
的距离.
推荐套卷
在四棱锥
中,侧面
底面
,侧棱
,底面
为直角梯形,其中
为
中点.
(Ⅰ)求证:
平面
;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点
到平面
的距离.
