（本小题满分13分）
在一次数学统考后，某班随机抽取10名同学的成绩进行样本分析，获得成绩数据的茎叶图如下．
（Ⅰ）计算样本的平均成绩及方差；
（Ⅱ）现从10个样本中随机抽出2名学生的成绩，设选出学生的分数为90分以上的人数为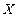
，求随机变量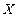的分布列和均值．
| 9 |
2 |
8 |
8 |
| 8 |
5 |
5 |
|
| 7 |
4 |
4 |
4 |
| 6 |
0 |
0 |
|
和曲线
在它们的交点处的两切线的夹角为
，求
。
上点
且与过这一点的切线垂直的直线的方程。
的切线中，斜率最小的切线的方程。
上任何一点
的切线与两坐标轴围成三角形面积是一个常数。
上有点
，用定义求：
处的切线的斜率；推荐套卷
（本小题满分13分）
在一次数学统考后，某班随机抽取10名同学的成绩进行样本分析，获得成绩数据的茎叶图如下．
（Ⅰ）计算样本的平均成绩及方差；
（Ⅱ）现从10个样本中随机抽出2名学生的成绩，设选出学生的分数为90分以上的人数为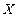，求随机变量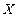的分布列和均值．
| 9 |
2 |
8 |
8 |
| 8 |
5 |
5 |
|
| 7 |
4 |
4 |
4 |
| 6 |
0 |
0 |
|
粤公网安备 44130202000953号