2014年11月10日APEC会议在北京召开,某服务部需从大学生中招收志愿者,被招收的志愿者需参加分笔试和面试两部分,把参加笔试的 40 名大学生的成绩分组: 第 1 组[75,80),第 2 组 [80,85),第 3 组[85, 90),第 4 组 [90, 95),第 5 组[95,100),得到频率分布直方图如图所示:
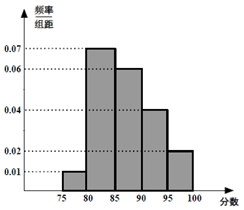
(Ⅰ)分别求成绩在第4,5组的人数;
(Ⅱ)现决定在笔试成绩较高的第 3,4,5 组中用分层抽样抽取 6 名进入面试,
①已知甲的成绩均在第4组,求甲进入面试的概率;
②若从这6名学生中随机抽取2名学生接受考官D的面试,设第3组中有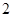 名学生被考官D面试的概率.
名学生被考官D面试的概率.