二次函数f(x)=ax2+x+1(a＞0)的图象与x轴的两个不同的交点的横坐标分别为x1、x2。
（1）证明：(1+x1)(1+x2)=1；
（2）证明：x1＜－1，x2＜－1；
（3）若函数y=xf(x)在区间（－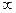
，－4）
上单调递增，试求a的取值范围。
相关试题
.
.
，那么x2＋2x－1≠0.
an＋n－4，λ∈R，n∈N＋，对任意λ相关知识点
推荐套卷
二次函数f(x)=ax2+x+1(a＞0)的图象与x轴的两个不同的交点的横坐标分别为x1、x2。
（1）证明：(1+x1)(1+x2)=1；
（2）证明：x1＜－1，x2＜－1；
（3）若函数y=xf(x)在区间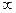（－，－4）上单调递增，试求a的取值范围。
粤公网安备 44130202000953号