已知：如图，射线OA为y=2x(x>0)，射线OB为y= –2x(x>0)，动点P（x, y）在
的内部，
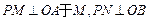于N，四边形ONPM的面积为2..
（I）动点P的纵坐标y是其横坐标x的函数，求这个函数y=f(x)的解析式；
（II）确定y=f(x)的定义域.
 |
相关知识点
推荐套卷
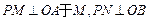已知：如图，射线OA为y=2x(x>0)，射线OB为y= –2x(x>0)，动点P（x, y）在的内部，于N，四边形ONPM的面积为2..
（I）动点P的纵坐标y是其横坐标x的函数，求这个函数y=f(x)的解析式；
（II）确定y=f(x)的定义域.
|
粤公网安备 44130202000953号