(1)设函数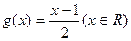 ,且数列
,且数列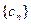 满足
满足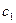 = 1,
= 1,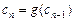 (n∈N,
(n∈N,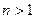 );求数列
);求数列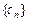 的通项公式.
的通项公式.
(2)设等差数列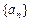 、
、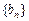 的前n项和分别为
的前n项和分别为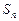 和
和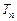 ,且
,且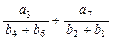
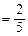 ,
,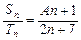 ,
, 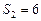 ;求常数A的值及
;求常数A的值及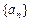 的通项公式.
的通项公式.
(3)若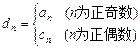 ,其中
,其中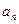 、
、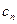 即为(1)、(2)中的数列
即为(1)、(2)中的数列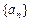 、
、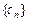 的第
的第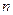 项,试求
项,试求
推荐套卷
(1)设函数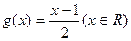 ,且数列
,且数列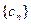 满足
满足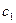 = 1,
= 1,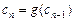 (n∈N,
(n∈N,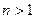 );求数列
);求数列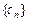 的通项公式.
的通项公式.
(2)设等差数列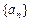 、
、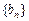 的前n项和分别为
的前n项和分别为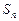 和
和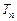 ,且
,且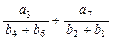
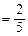 ,
,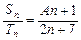 ,
, 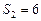 ;求常数A的值及
;求常数A的值及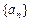 的通项公式.
的通项公式.
(3)若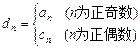 ,其中
,其中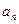 、
、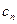 即为(1)、(2)中的数列
即为(1)、(2)中的数列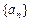 、
、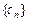 的第
的第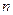 项,试求
项,试求