设f(x)=x3+3x2+px, g(x)=x3+qx2+r，且y=f(x)与y=g(x)的图象关于点（0，1）对称．（1）求p、q、r的值；（2）若函数g(x)在区间(0，m)上递减，求m的取值范围；（3）若函数g(x)在区间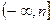
上的最大值为2，求n的取值范围．
相关试题
，
．
的最大值，并求出当
的取值；
的值；
，且
，求
的值．
中，
，证明数列
是等比数列并求数列
项和
}的前n 项和为
，已知
成等差数列
的公比
；
，求
点D是AB的中点，
推荐套卷
设f(x)=x3+3x2+px, g(x)=x3+qx2+r，且y=f(x)与y=g(x)的图象关于点（0，1）对称．（1）求p、q、r的值；（2）若函数g(x)在区间(0，m)上递减，求m的取值范围；（3）若函数g(x)在区间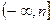 上的最大值为2，求n的取值范围．
粤公网安备 44130202000953号