对于函数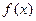
，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数f(x)＝
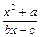有且仅有两个不动点0和2．
(Ⅰ)试求b、c满足的关系式；
(Ⅱ)若c＝2时，各项不为零的数列{an}满足4Sn·f(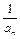
)＝1，
求证：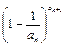
＜
＜
；
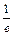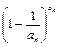(Ⅲ)设bn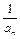＝－，Tn为数列{bn}的前n项和，求证：T2009－1＜ln2009＜T2008．
相关试题
是平行四边形
所在平面外的一点，
、
分别是
、
上的点且
，求证：
平面
．
，问是否存在斜率为
的直线
，使以
截得的弦
为直径的圆经过原点．若存在，写出直线
及
，对角线的交点是
，求另两边所在直线的方程．
+
+
≥
+
+
．
相交于点M，在OM上取一点P，使得
，求点P的轨迹的极坐标方程．推荐套卷
对于函数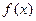，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数f(x)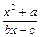＝有且仅有两个不动点0和2．
(Ⅰ)试求b、c满足的关系式；
(Ⅱ)若c＝2时，各项不为零的数列{an}满足4Sn·f(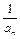)＝1，
求证：＜＜；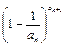
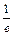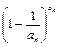(Ⅲ)设bn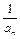＝－，Tn为数列{bn}的前n项和，求证：T2009－1＜ln2009＜T2008．
粤公网安备 44130202000953号