已知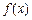 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且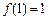 ,若任意的
,若任意的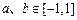 ,当
,当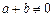 时,总有
时,总有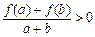 .
.
(1)判断函数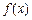 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式: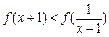 ;
;
(3)若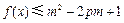 对所有的
对所有的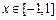 恒成立,其中
恒成立,其中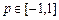 (
(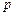 是常数),求实数
是常数),求实数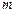 的取值范围.
的取值范围.
推荐套卷
已知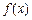 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且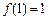 ,若任意的
,若任意的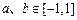 ,当
,当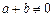 时,总有
时,总有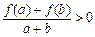 .
.
(1)判断函数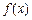 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式: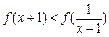 ;
;
(3)若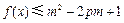 对所有的
对所有的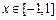 恒成立,其中
恒成立,其中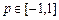 (
(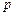 是常数),求实数
是常数),求实数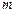 的取值范围.
的取值范围.