在等差数列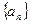 中,
中, ,
,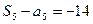 ,其中
,其中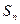 是数列
是数列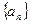 的前
的前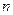 项之和,曲线
项之和,曲线 的方程是
的方程是 ,直线
,直线 的方程是
的方程是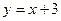 .
.
(1) 求数列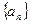 的通项公式;
的通项公式;
(2) 当直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点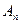 ,
,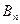 时,令
时,令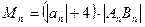 ,
,
求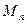 的最小值;
的最小值;
(3) 对于直线 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.
推荐套卷
在等差数列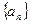 中,
中, ,
,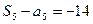 ,其中
,其中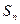 是数列
是数列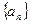 的前
的前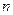 项之和,曲线
项之和,曲线 的方程是
的方程是 ,直线
,直线 的方程是
的方程是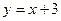 .
.
(1) 求数列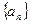 的通项公式;
的通项公式;
(2) 当直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点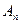 ,
,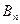 时,令
时,令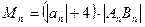 ,
,
求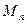 的最小值;
的最小值;
(3) 对于直线 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.