在平面直角坐标系中，△ABC的两个顶点A，B的坐标分别为A（－1，0），B（1，0），平面
内两点G，M同时满足下列条件①
＋
＋
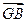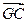＝0；②｜
｜＝｜
｜＝｜
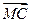｜；③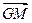
∥
.（Ⅰ）求△ABC的顶点C的轨迹方程；（Ⅱ）是否存在过点P（3，0）的直线l与（Ⅰ）中轨迹交于E、F两点，且OE⊥OF?若存在，求出直线l斜率k的值；若不存在，说明理由．
相关试题
，
，
，且
是
的充分不必要条件，求
的取值范围．
，当
时满足
，
，求数列
的前n项和
．
，
，函数
．
的解析式；
与
具有完全相同的单调区间，求
的值；
时恒有
求
，当
时满足
，
，求数列
的前n项和
．推荐套卷
在平面直角坐标系中，△ABC的两个顶点A，B的坐标分别为A（－1，0），B（1，0），平面
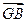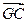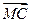内两点G，M同时满足下列条件①＋＋＝0；②｜｜＝｜｜＝｜｜；③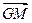∥.（Ⅰ）求△ABC的顶点C的轨迹方程；（Ⅱ）是否存在过点P（3，0）的直线l与（Ⅰ）中轨迹交于E、F两点，且OE⊥OF?若存在，求出直线l斜率k的值；若不存在，说明理由．
粤公网安备 44130202000953号