已知函数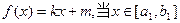 时,
时,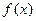 的值域为
的值域为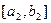 ,当
,当
时,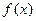 的值域为
的值域为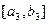 ,依次类推,一般地,当
,依次类推,一般地,当 时,
时,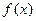 的值域为
的值域为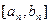 ,其中k、m为常数,且
,其中k、m为常数,且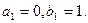
(1)若k=1,求数列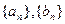 的通项公式;
的通项公式;
(2)项m=2,问是否存在常数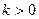 ,使得数列
,使得数列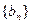 满足
满足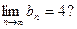 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;
(3)若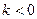 ,设数列
,设数列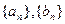 的前n项和分别为Sn,Tn,求
的前n项和分别为Sn,Tn,求 。
。
推荐套卷
已知函数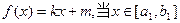 时,
时,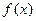 的值域为
的值域为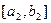 ,当
,当
时,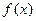 的值域为
的值域为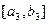 ,依次类推,一般地,当
,依次类推,一般地,当 时,
时,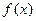 的值域为
的值域为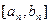 ,其中k、m为常数,且
,其中k、m为常数,且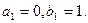
(1)若k=1,求数列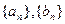 的通项公式;
的通项公式;
(2)项m=2,问是否存在常数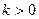 ,使得数列
,使得数列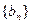 满足
满足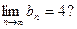 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;
(3)若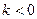 ,设数列
,设数列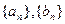 的前n项和分别为Sn,Tn,求
的前n项和分别为Sn,Tn,求 。
。