高考数学试题中共有12道选择题每道选择题都有4个选项,其中有且仅有一个是正确的。评分标准规定:“每题只选1项,答对得5分,不答或答错得0分”,某考生每道题都给出了一个答案,已确定有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(Ⅰ)选择题没得60分的概率;(Ⅱ)选择题所得分数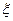 的数学期望.( 保留三位有效数字)
的数学期望.( 保留三位有效数字)
推荐套卷
高考数学试题中共有12道选择题每道选择题都有4个选项,其中有且仅有一个是正确的。评分标准规定:“每题只选1项,答对得5分,不答或答错得0分”,某考生每道题都给出了一个答案,已确定有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(Ⅰ)选择题没得60分的概率;(Ⅱ)选择题所得分数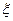 的数学期望.( 保留三位有效数字)
的数学期望.( 保留三位有效数字)