某班有50名学生，在学校组织的一次数学质量抽测中，如果按照抽测成绩的分数段［60，65），［65，70），…,［95，100）进行分组，得到的分布情况如图3所示.求：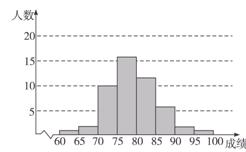
图3
（1）该班抽测成绩在［70，85）之间的人数；
（2）该班抽测成绩不低于85分的人数占全班总人数的百分比.
相关试题
，满足
的解析式
时，求函数
的值是5，则输出的
值是多少？
（
为参数）被双曲线
所截得的弦长。
的值；
，求
的值；
在
上的最小值．
关于时间
的函数表达式（
与时间
，相关知识点
推荐套卷
某班有50名学生，在学校组织的一次数学质量抽测中，如果按照抽测成绩的分数段［60，65），［65，70），…,［95，100）进行分组，得到的分布情况如图3所示.求：
图3
（1）该班抽测成绩在［70，85）之间的人数；
（2）该班抽测成绩不低于85分的人数占全班总人数的百分比.
粤公网安备 44130202000953号