已知双曲线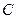 的中心在原点,对称轴为坐标轴,其一条渐近线方程是
的中心在原点,对称轴为坐标轴,其一条渐近线方程是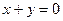 ,且双曲线
,且双曲线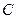 过点
过点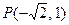 .
.
(1)求此双曲线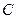 的方程;
的方程;
(2)设直线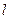 过点
过点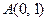 ,其方向向量为
,其方向向量为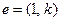
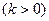 ,令向量
,令向量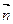 满足
满足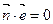 .双曲线
.双曲线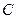 的右支上是否存在唯一一点
的右支上是否存在唯一一点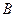 ,使得
,使得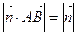 . 若存在,求出对应的
. 若存在,求出对应的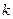 值和
值和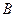 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
相关知识点
推荐套卷
已知双曲线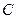 的中心在原点,对称轴为坐标轴,其一条渐近线方程是
的中心在原点,对称轴为坐标轴,其一条渐近线方程是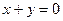 ,且双曲线
,且双曲线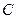 过点
过点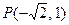 .
.
(1)求此双曲线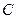 的方程;
的方程;
(2)设直线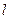 过点
过点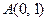 ,其方向向量为
,其方向向量为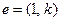
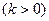 ,令向量
,令向量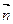 满足
满足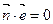 .双曲线
.双曲线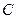 的右支上是否存在唯一一点
的右支上是否存在唯一一点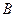 ,使得
,使得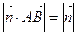 . 若存在,求出对应的
. 若存在,求出对应的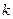 值和
值和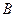 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.