一用户到电信局打算上网开户,经询问,有三种月消费方式:(1)163普通方式:上网资费2元/小时;(2)163A方式:每月30元(可上网50小时),超过50小时以上的资费为 2元/小时;(3) ADLSD方式:每月50元,时长不限(其它因素均忽略不计)。(每月以30日计算)
(1)、分别写出三种上网方式中所用月资费( )与时间(
)与时间(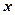 )的函数关系式;
)的函数关系式;
(2)、在同一坐标系内画出三种上网方式中所用资费与时间的函数图象;
(3)、根据你的研究,给这一用户一个合理化的建议。
推荐套卷
一用户到电信局打算上网开户,经询问,有三种月消费方式:(1)163普通方式:上网资费2元/小时;(2)163A方式:每月30元(可上网50小时),超过50小时以上的资费为 2元/小时;(3) ADLSD方式:每月50元,时长不限(其它因素均忽略不计)。(每月以30日计算)
(1)、分别写出三种上网方式中所用月资费( )与时间(
)与时间(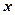 )的函数关系式;
)的函数关系式;
(2)、在同一坐标系内画出三种上网方式中所用资费与时间的函数图象;
(3)、根据你的研究,给这一用户一个合理化的建议。