若动圆P恒过定点B（2，0），且和定圆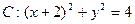
外切.
（1）求动圆圆心P的轨迹E的方程；
（2）若过点B的直线l与曲线E交于M、N两点，试判断以MN为直径的圆与直线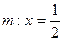
是否相交，若相交，求出所截得劣弧的弧度数，若不相交，请说明理由.
}满足a
=1，a
a
+1（n≥2），求数列{a
前n项和
.
与
的关系；（2）求通项公式
中，
,
，求
。
，
，求
。
：
，求
.推荐套卷
若动圆P恒过定点B（2，0），且和定圆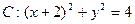外切.
（1）求动圆圆心P的轨迹E的方程；
（2）若过点B的直线l与曲线E交于M、N两点，试判断以MN为直径的圆与直线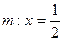 是否相交，若相交，求出所截得劣弧的弧度数，若不相交，请说明理由.
粤公网安备 44130202000953号