(本小题满分12分)标准椭圆 的两焦点为
的两焦点为 ,
, 在椭圆上,且
在椭圆上,且 . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线 的方向向量为
的方向向量为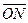 ,若
,若 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
推荐套卷
(本小题满分12分)标准椭圆 的两焦点为
的两焦点为 ,
, 在椭圆上,且
在椭圆上,且 . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线 的方向向量为
的方向向量为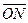 ,若
,若 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.