（本小题满分12分）将一个质地均匀的正方体（六个面上分别标有数字0，1，2，3，4，5）和一个正四面体（四个面分别标有数字1，2，3，4）同时抛掷1次，规定“正方体向上的面上的数字为a，正四面体的三个侧面上的数字之和为b”。设复数为
（1）若集合
，用列举法表示集合A；（2）求事件“复数在复平面内对应的点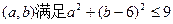
”的概率。
相关试题
，
在
上是增函数。
，
轴上，离心率
的角平分线所在直线的方程
建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙(利用旧墙需维修)，其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用的旧墙的长度为x(单位：m),修建此矩形场地围墙的总费用为y(单位：元)
推荐套卷
（本小题满分12分）将一个质地均匀的正方体（六个面上分别标有数字0，1，2，3，4，5）和一个正四面体（四个面分别标有数字1，2，3，4）同时抛掷1次，规定“正方体向上的面上的数字为a，正四面体的三个侧面上的数字之和为b”。设复数为 （1）若集合，用列举法表示集合A；（2）求事件“复数在复平面内对应的点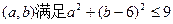”的概率。
粤公网安备 44130202000953号