有甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在此岸边合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，问供水站C建在岸边何处才能使水管费用最省？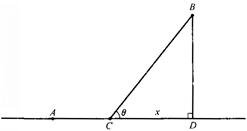
与抛物线
在它们一个交点处的切线互相垂直，求
与
之间的关系。
上有点
，与曲线切于点
的切线为
，若直线
过
轴于点
，又作
轴于
，求
的长。
与曲线
相切，试求
的值。
，求与
都相切的直线
的方程。
上点
且与过
点的切线夹角最大的直线的方程。推荐套卷
有甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在此岸边合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，问供水站C建在岸边何处才能使水管费用最省？
粤公网安备 44130202000953号