（本小题满分12分）已知双曲线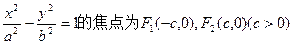
，焦点F2到渐近线的距离为
，两条准线之间的距离为1。 （I）求此双曲线的方程； （II）过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点，过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点，若A、B、C、D这四点依次构成平行四边形ABCD，且
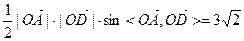，求直线AB的方程。
处的切线与直线
平行；
的单调区间；
，求函数
单调区间；
在区间（1，2）单调递减。
时，求a的取值范围；
的取值范围。
的图像按向量a=（2，—1）平移后，再作关于直线y=x的对称图像
推荐套卷
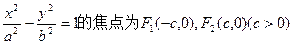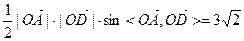（本小题满分12分）已知双曲线，焦点F2到渐近线的距离为，两条准线之间的距离为1。 （I）求此双曲线的方程； （II）过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点，过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点，若A、B、C、D这四点依次构成平行四边形ABCD，且，求直线AB的方程。
粤公网安备 44130202000953号