A.选修4 - 1:几何证明选讲
如图,在四边形
中,
.
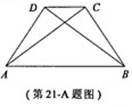
求证:
.
B.选修4 - 2:矩阵与变换
求矩阵
的逆矩阵.
C.选修4 - 4:坐标系与参数方程
已知曲线
的参数方程为
(
为参数,
),求曲线
的普通方程.
D.选修4 - 5:不等式选讲
设
,求证:
.
推荐套卷
A.选修4 - 1:几何证明选讲
如图,在四边形
中,
.

求证:
.
B.选修4 - 2:矩阵与变换
求矩阵
的逆矩阵.
C.选修4 - 4:坐标系与参数方程
已知曲线
的参数方程为
(
为参数,
),求曲线
的普通方程.
D.选修4 - 5:不等式选讲
设
,求证:
.