（本小题满分13分，（Ⅰ）问7分，（Ⅱ）问6分）
某单位为绿化环境，移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为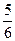
和
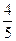，且各株大树是否成活互不影响。求移栽的4株大树中：
（Ⅰ）至少有1株成活的概率；
（Ⅱ）两种大树各成活1株的概率。
相关试题
是奇函数，
的值；
，求
的值.
中，角A、B、C所对的边分别为
，且
，
的值；
，求
满足
，且
，
为
项和．
，不等式
恒成立，求实数
的取值范围．
．
时，不等式
恒成立，求实数
的取值范围；
在区间
上的最大值．
中，
平面
，其垂足
落在直线
上．
⊥
；
，
，
为
的中点，求二面角
的平面角的余弦值．推荐套卷
（本小题满分13分，（Ⅰ）问7分，（Ⅱ）问6分）
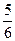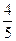某单位为绿化环境，移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响。求移栽的4株大树中：
（Ⅰ）至少有1株成活的概率；
（Ⅱ）两种大树各成活1株的概率。
粤公网安备 44130202000953号