如图，某建筑物的基本单元可近似地按以下方法构作：先在地平面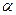
内作菱形ABCD，边长为1，∠BAD＝60°,再在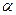的上方，分别以△
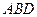与△
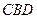为底面安装上相同的正棱锥P－ABD与Q－CBD，∠APB＝90°．
（Ⅰ）求证：PQ⊥BD；
（Ⅱ）求二面角P-BD-Q的余弦值；
（Ⅲ）求点P到平面QBD的距离.
相关试题
；
；
．
在[1，+∞
上为增函数.
的大小，说明理由；
（n∈N*, n≥2）
中，
侧面
，
为棱
上异于
的一点，
，已知
，求：
与
的距离；
的平面角的正切值.推荐套卷
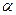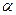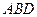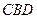如图，某建筑物的基本单元可近似地按以下方法构作：先在地平面内作菱形ABCD，边长为1，∠BAD＝60°,再在的上方，分别以△与△为底面安装上相同的正棱锥P－ABD与Q－CBD，∠APB＝90°．
（Ⅰ）求证：PQ⊥BD；
（Ⅱ）求二面角P-BD-Q的余弦值；
（Ⅲ）求点P到平面QBD的距离.
粤公网安备 44130202000953号