已知直线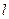
过点M（1，2），且直线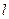与x轴正半轴和y轴的正半轴交点分别是A、B，（如图，注意直线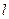与坐标轴的交点都在正半轴上）
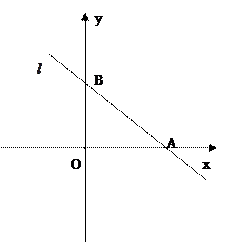（1）若三角形AOB的面积是4，求直线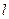的方程。
（2）求过点N（0，1）且与直线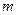
垂直的直线方程。
相关试题
满足
，则称
为
的不动点．
没有不动点，求实数
的取值范围；
的不动点
，求
的值；
有不动点，求实数
中，底面
是边长为
的菱形，
，
面
，
，
分别为
，
的中点．
面
；
的大小的正弦值；
到面
中，角
所对的边为
．已知
，且
．
的值；
时，求
．
为等差数列
的前
项和，已知
．
；
．
的图象过原点，且对
，恒有
．设数列
满足
．
；
．推荐套卷
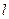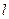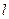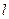已知直线过点M（1，2），且直线与x轴正半轴和y轴的正半轴交点分别是A、B，（如图，注意直线与坐标轴的交点都在正半轴上）（1）若三角形AOB的面积是4，求直线的方程。
（2）求过点N（0，1）且与直线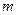垂直的直线方程。
粤公网安备 44130202000953号