已知函数f(x)＝alnx＋bx,且f(1)＝－1，f′(1)＝0，
⑴求f(x)；
⑵求f(x)的最大值；
⑶若x＞0,y＞0,证明：lnx＋lny≤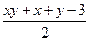
.
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．
相关试题
的值为最小
最小。
的方程为
，求直线
的方程，使得：（1）
；（2）
的顶点为
，
，
，
，求证：四边形推荐套卷
已知函数f(x)＝alnx＋bx,且f(1)＝－1，f′(1)＝0，
⑴求f(x)；
⑵求f(x)的最大值；
⑶若x＞0,y＞0,证明：lnx＋lny≤.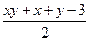
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．
粤公网安备 44130202000953号