已知长方体ABCD—A1B1C1D1中，AB=BC=4，AA1=8，E、F分别为AD和CC1的中点，O1为下底面正方形的中心。
（Ⅰ）证明：AF⊥平面FD1B1；
（Ⅱ）求异面直线EB与O1F所成角的余弦值；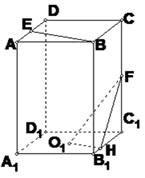 
相关试题
，焦点为F，顶点为O，点P在抛物线上移动，Q是OP的中点，M是FQ的中点，求点M的轨迹方程.
：方程
有两个不相等的负实根，命题
：方程
无实根；若
的取值范围．
，直线
.椭圆上是否存在一点，它到直线
的距离最小？最小距离是多少？
线的渐近线方程为y＝±x，并且焦点都在圆x2＋y2＝100上，求双曲线方程．
，深为3
.如果池底每平方米的造价为150元，池壁每平方米的造价为
120元，怎样设计水池能使总造价最低？最低造价是多少？推荐套卷
已知长方体ABCD—A1B1C1D1中，AB=BC=4，AA1=8，E、F分别为AD和CC1的中点，O1为下底面正方形的中心。
（Ⅰ）证明：AF⊥平面FD1B1；
（Ⅱ）求异面直线EB与O1F所成角的余弦值；
粤公网安备 44130202000953号