如图，直角梯形ABCE中，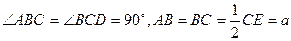
，D是CE的中点，点M和点N在
ADE绕AD向上翻折的过程中，分别以
的速度，同时从点A和点B沿AE和BD各自匀速行进，t 为行进时间，0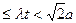
。
（1） 求直线AE与平面CDE所成的角；
（2） 求证：MN//平面CDE。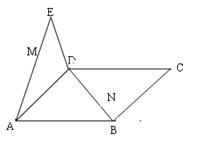
，设
．
时，求z的取值范围．
（
），且
的最大值为7，求k的值．
．
；
，
，
中至少有一个不小于
．
的最大值．
，
，求证：
．推荐套卷
如图，直角梯形ABCE中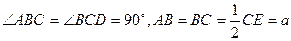，，D是CE的中点，点M和点N在ADE绕AD向上翻折的过程中，分别以的速度，同时从点A和点B沿AE和BD各自匀速行进，t 为行进时间，0。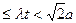
（1） 求直线AE与平面CDE所成的角；
（2） 求证：MN//平面CDE。
粤公网安备 44130202000953号