如图a—l—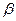 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在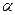 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在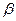 内,
内,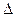 ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=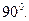
(I) 求三棱锥D—ABC的体积;
(2)求二面角D—AC—B的大小;
(3)求异面直线AB、CD所成的角.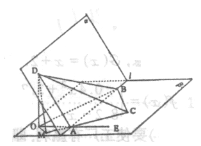
推荐套卷
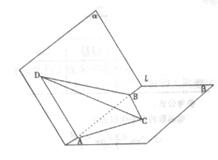
如图a—l—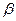 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在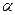 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在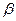 内,
内,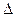 ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=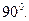
(I) 求三棱锥D—ABC的体积;
(2)求二面角D—AC—B的大小;
(3)求异面直线AB、CD所成的角.
