四棱锥P—ABCD中，PA⊥面ABCD，PA=AB=BC=2，E为PA中点，过E作平行于底面的面EFGH分别与另外三条侧棱交于F，G，H，已知底面ABCD为直角梯形，AD//BC，AB⊥AD，∠BCD=135°
（1）求异面直线AF，BG所成的角的大小；
（2）设面APB与面CPD所成的锐二面角的大小为θ，求cosθ.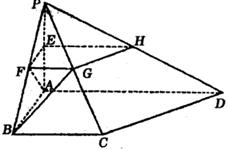
相关试题
，函数
的定义域为
，
．
．
的左焦点
为圆
的圆心，且椭圆上的点到点
．
与椭圆交于不同的两点
，点
，求
的值．
中,角
，所对的边分别是
，且
．
的值；
，求
面积的最大值．
的各项均为正数，
是数列
．
的通项公式；
的值．
．
的解集
．求
的值；
．求
的最小值．推荐套卷
四棱锥P—ABCD中，PA⊥面ABCD，PA=AB=BC=2，E为PA中点，过E作平行于底面的面EFGH分别与另外三条侧棱交于F，G，H，已知底面ABCD为直角梯形，AD//BC，AB⊥AD，∠BCD=135°
（1）求异面直线AF，BG所成的角的大小；
（2）设面APB与面CPD所成的锐二面角的大小为θ，求cosθ.
粤公网安备 44130202000953号